Compound Inequalities
A compound inequality is an equation with two or more inequalities joined together with either “and” or “or”. For example: x ≤ -3 or x ≥ 2; x ≥ -7 and x ≤ 7

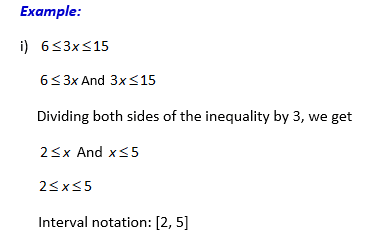
ii) 2(y-1) < 6 Or 2(y-1) > 10
These inequalities are connected with < or > symbol, so the solution will be the union of solutions of these two inequalities.
Dividing both sides by 2,
(y-1) < 3 or (y-1) > 5
Adding 1 to both sides of the inequality, we get
y<4 Or y>6
Interval notation: ![]()
Check Point
Solve the given compound inequalities and write the answer in interval notation:
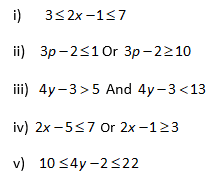
Answer Key

There is no overlap between the two inequalities, hence there is no solution to the compound inequality.



