Solve System of Linear Equations with Elimination and Substitution
Grade 8 Math Worksheets

Schedule a Free session to clear worksheet doubts
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Let’s see this with the help of an example –
3x – 4y = 11 …Equation (1)
-3x + 2y = -7 …Equation (2)
When we add the two equations, x-terms will be eliminated. This happens because the coefficients of the x-terms, 3 and -3, are opposites of each other.
So, adding we get:
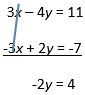
Dividing both sides by -2, we get, y = -2
Now put y = -2 back in equation (1) or equation (2) to get the value of x. Let us put y = -2 in equation (1):
3x – 4(-2) = 11 3x + 8 = 11
3x = 11 – 8 3x = 3
x = 1
Check the solution: Put x = 1 and y = -2 in the given equations to check the answer.
Left Hand Side (L.H.S) of the equation 3x – 4y = 11:
3(1) – 4(-2) = 3 + 8 = 11, which is the same as right Hand Side (R.H.S) of the equation.
Since L.H.S = R.H.S, so the values are correct.
Similarly, L.H.S of the equation -3x + 2y = -7:
-3(1) + 2(-2) = -3 – 4 = -7, which is the same as R.H.S of the equation.
Since L.H.S = R.H.S, so the values are correct.
Personalized Online Tutoring from eTutorWorld
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades K-12, Test Prep help for Standardized tests like SCAT, CogAT, MAP, SSAT, SAT, ACT, ISEE and AP. You may schedule online tutoring lessons at your personal scheduled times, all with a Money-Back Guarantee. The first one-on-one online tutoring lesson is always FREE, no purchase obligation, no credit card required.
For answers/solutions to any question or to learn concepts, take a FREE TRIAL Session.
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Example: Solve the given system of equations by elimination method –
5x – 4y = 9 …Equation (1)
x – 2y = -3 …Equation (2)
Here we can either multiply equation (2) by 5 so that the coefficient of x in equation (2) is also 5 and then we can subtract both the equations to get the value of y, or we can multiply equation (2) by ‘-2’ and then add the two equations to get the value of x.
Here we multiply equation (2) by -2, and then add the equations –
5x – 4y = 9 …Equation (1) ——————— 5x – 4y = 9 …Equation (1)
x – 2y = -3 …Equation (2) ——————— -2x + 4y = 6 …Equation (2)
Adding the equations we get, 5x – 2x = 9 + 6
3x = 15
Dividing by 3 we get, x = 5
Put this value of x = 5 in any of the two equations to get the value of y, putting x = 5 in equation (2) we get:
5 – 2y = -3
2y = 5 + 3
2y = 8 implies y = 4
Check the solution:
L.H.S of the equation 5x – 4y = 9:
5(5) – 4(4) = 25 – 16 = 9, which is equal to the R.H.S of the equation.
L.H.S of the equation x – 2y = -3:
5 – 2(4) = 5 – 8 = -3, which is equal to the R.H.S of the equation.

Example: Solve the following equations for x and y:
2x + y = 3 …Equation (1)
-5x + y = -4 …Equation (2)
Step 1: From equation (1), y = 3 – 2x
Step 2 and 3: Put y = 3 – 2x in equation (2), –5x + (3 – 2x) = -4
-5x – 2x = -4 – 3
-7x = -7 ⇒ x = 1
Step 4: Put x = 1 in equation (1), y = 3 – 2x
y = 3 – 2(1)
y = 3 – 2
y = 1
Step 5: Check the solution: Put x = 1 and y = 1 in any of the given equations to check the answer.
Left Hand Side (L.H.S) of the equation 2x + y = 3:
2(1) + 1 = 2 + 1 = 3, which is equal to the R.H.S of the equation.
Since L.H.S = R.H.S so, the values are correct.
L.H.S of -5x + y = -4:
-5(1) + 1 = -5 + 1 = -4, which is equal to the R.H.S of the equation.
Since L.H.S = R.H.S so, the values are correct.
Check Point
- Solve by elimination method:
x + y = 1
x – y = 3
- Solve by substitution method:
x + 2y = 2
-4x + 3y = 25
- Solve by elimination method:
2x + 5y = -4
3x – y = 11
- Solve by substitution method:
5x + 2y = 0
x – 3y = 0
- Solve by elimination method:
x = 4y – 2
x = 6y + 8
Answer key
- (2, -1)
- (-4, 3)
- (3, -2)
- (0, 0)
- (-22, -5)
Schedule a Free session to clear worksheet doubts
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Learn more about Scientific Method and other important topics with 7th Grade Science Tutoring at eTutorWorld. Our expert science tutors break down the topics through interactive one-to-one sessions. We also offer the advantage of customized lesson plans, flexible schedules and convenience of learning from home.
Pricing for Online Tutoring
| Tutoring Package | Validity | Grade (1-12), College |
|---|---|---|
| 5 sessions | 1 Month | $124 |
| 1 session | 1 Month | $25 |
| 10 sessions | 3 months | $239 |
| 15 sessions | 3 months | $354 |
| 20 sessions | 4 months | $449 |
| 50 sessions | 6 months | $1049 |
| 100 sessions | 12 months | $2049 |


